Журнал «Травма» Том 14, №2, 2013
Вернуться к номеру
Сравнительный теоретический анализ биомеханических аспектов остеосинтеза при поперeчном переломе большеберцовой кости контактными и малоконтактными пластинами (Сообщение первое)
Авторы: Билинский П.И., Чаплинский В.П., Андрейчин В.А., Национальная медицинская академия последипломного образования им. П.Л. Шупика, г. Киев, Центральная районная больница, г. Самбор
Ивано-Франковский национальный медицинский университет
Рубрики: Ревматология, Травматология и ортопедия
Разделы: Клинические исследования
Версия для печати
Представлены результаты твердотельного моделирования и конечноэлементного анализа большеберцовой кости, синтезированной полноконтактным одноплоскостным и малоконтактным многоплоскостным фиксаторами при наличии поперечного перелома. Выполнено сопоставление двух способов фиксации с точки зрения восприятия физиологических нагрузок.
Исследования показали, что малоконтактный многоплоскостной фиксатор имеет значительно больше преимуществ в сравнении с полноконтактным одноплоскостным. Он исключает переход микроподвижности фрагментов в макроперемещение при нагрузке, испытывает меньшее напряжение, а также устраняет давление пластины на кость.
Наведено результати твердотілого моделювання і кінцевоелементного аналізу великої гомілкової кістки, синтезованої повноконтактним одноплощинним і малоконтактним багатоплощинним фіксаторами за наявності поперечного перелому. Виконано зіставлення двох способів фіксації з точки зору сприйняття фізіологічних навантажень.
Дослідження показали, що малоконтактний багатоплощинний фіксатор має значно більше переваг порівняно з повноконтактним одноплощинним. Він виключає перехід мікрорухливості фрагментів в макропереміщення при навантаженні, отримує менше напруження, а також усуває тиск пластини на кістку.
The results of solid modelling and finite element analysis of tibia, synthesized with full-contact with single-plane and limited-contact multiplane fixators in the presence of traverse fracture. Comparison of the both methods of fixation has been carried out in terms of perception of physiologic stress.
The researches had shown that limited-contact multiplane fixator has much more advantages in comparison with a full-contact single-plane fixator. It excludes the change of fragments micromotion into macromotion in loading, has smaller stress and removes plate pressure on the bone.
перелом голени, малоконтактный многоплоскостной остеосинтез, метод конечных элементов.
перелом гомілки, малоконтактний багатоплощинний остеосинтез, метод кінцевих елементів.
tibial fracture, limited-contact multiplane osteosynthesis, finite element method.
Введение
Создание и совершенствование устройств для фиксации переломов конечностей основывается на результатах многочисленных исследований в различных направлениях. Одно из таких направлений составляет теоретическое изучение особенностей деформирования кости совместно с фиксатором под действием характерных физиологических нагрузок. Достижение максимального клинического эффекта предполагает рациональный выбор материала и конструкции фиксатора, а также способа его крепления на кость. При этом цель состоит в обеспечении необходимых прочностных и жесткостных характеристик, а также надежности фиксации совместно с микроподвижностью в зоне перелома в течение всего восстановительного периода. Существенными факторами являются также габариты и масса фиксатора, простота установки и снятия, а также степень травматичности для кости. Преимущество того или иного варианта остеосинтеза может быть оценено на основе анализа статистики клинического применения, при этом обоснованные выводы требуют большого количества наблюдений в течение продолжительного периода. Более доступный и менее затратный путь основывается на теоретическом исследовании механических аспектов фиксации с использованием современных средств компьютерного моделирования и анализа. Этот подход позволяет априорно, т.е. на стадии планирования операции, выбрать наилучший вариант конструкции фиксатора и способа его установки на сломанную кость.
Материалы и методы
Традиционным способом остеосинтеза поперечных переломов большеберцовой кости является полноконтактная фиксация, при которой пластина крепится на кости с помощью шурупов, расположенных в одной плоскости. Альтернативный способ (малоконтактная многоплоскостная фиксация) состоит в установке на кость фиксирующей пластины посредством промежуточных элементов в виде полукольцевых захватов, при этом шурупы, скрепляющие с костью как захваты, так и собственно пластину, располагаются в разных плоскостях. Полукольца крепятся к пластине с помощью винтов. Кроме этого, между полукольцами и шурупами имеется резьбовое взаимодействие, что предупреждает свободное перемещение шурупа при лизисе кости и нагрузке, препятствует отходу пластины от кости. Такой фиксатор устраняет давление пластины на кость, обеспечивает создание стабильной биомеханической конструкции «фиксатор — кость». Количественной оценке подлежит подвижность фрагментов сломанной кости, а также уровень напряженного состояния фиксатора и кости при нагрузке.
Сложность геометрии изучаемых объектов исключает возможность аналитического решения задачи исследования напряженно-деформированного состояния (н.д.с.) и допускает применение только численных методов. Наиболее универсальным среди них является метод конечных элементов (МКЭ).
В основе МКЭ лежит идея полиномиальной аппроксимации искомых неизвестных в пределах отдельных конечных элементов — малых непересекающихся областей, на которые разбивается исследуемый объект. Коэффициентами упомянутых полиномов, называемых функциями формы, являются значения искомых величин в узловых точках конечного элемента [2, 5], т.е. степень полинома в каждом элементе определяется количеством узлов.
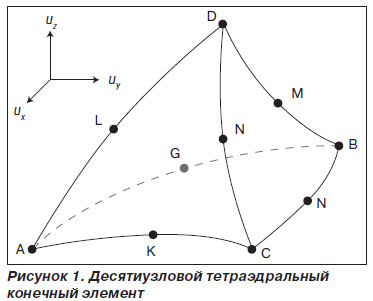
При решении пространственных задач универсальный конечный элемент, пригодный для дискретизации трехмерных тел произвольной формы, представляет собой четырехгранную пирамиду — тетраэдр. Элемент, показанный на рис. 1, помимо четырех узлов в вершинах содержит также узлы на серединах ребер. Теперь аппроксимация каждой компоненты перемещения, в том числе ux, в пределах элемента может быть выражена через 10 узловых значений и поэтому представляется зависимостью, содержащей 10 коэффициентов [5]:
ux (x, y, z) = a0 + а1х + а2у + а3z + а4х2 + а5у2 + а6z2 + а7ху + а8хz + а9yz, (1)
т.е. 10-узловой элемент описывается квадратичными функциями формы. Функции формы определяют и геометрию самого элемента.
Для численного решения на основе МКЭ задачи об упругом деформировании трехмерного тела создана объемная модель, отражающая наиболее существенные особенности геометрии оригинала. С этой целью использованы средства твердотельного моделирования.
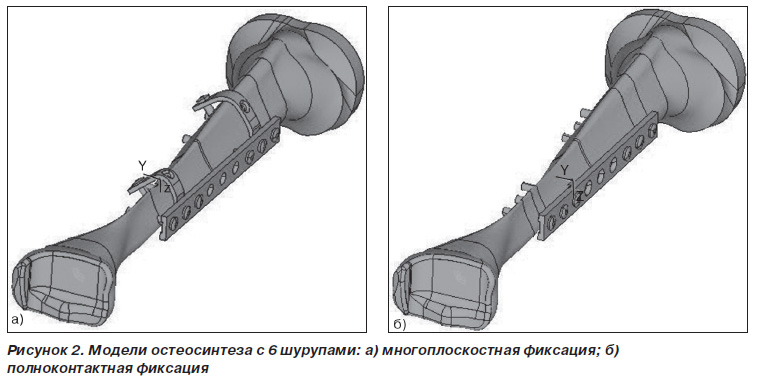
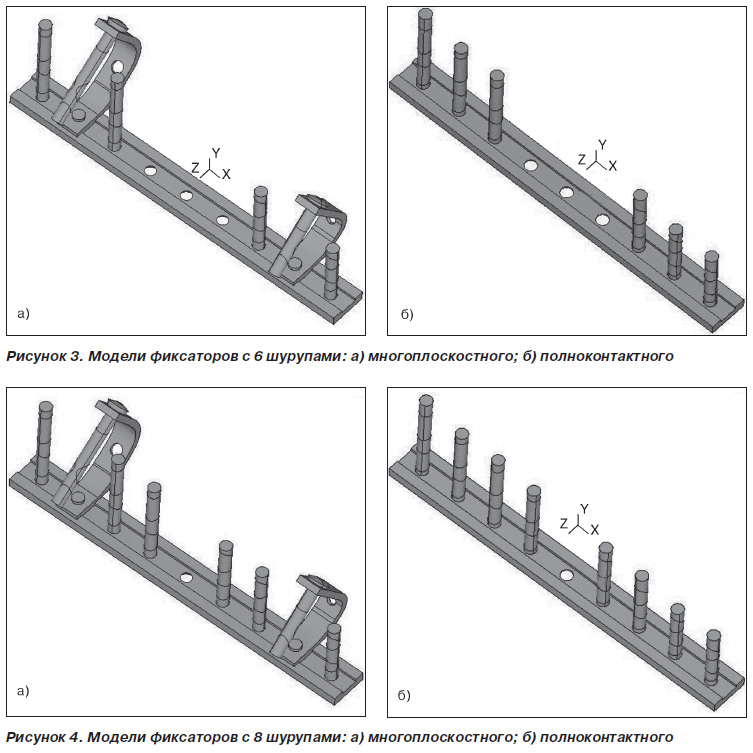
Рассматривается случай поперечного перелома в центральной части большеберцовой кости. Осевой зазор между торцевыми поверхностями фрагментов в месте перелома составляет 1,5 мм. Модели, имитирующие сломанную кость с установленными фиксаторами двух модификаций, показаны на рис. 2. Требование сопоставимости двух способов фиксации предполагает идентичность моделей, в том числе размеров планки и ее расположения относительно места перелома, а также числа крепежных деталей. В частности, предусмотрено крепление фиксатора шестью шурупами: по три с каждой стороны перелома, в том числе по одному шурупу — для стыковки с костью полукольцевых захватов при многоплоскостной фиксации. Модели фиксаторов вместе с крепежными деталями изображены на рис. 3.
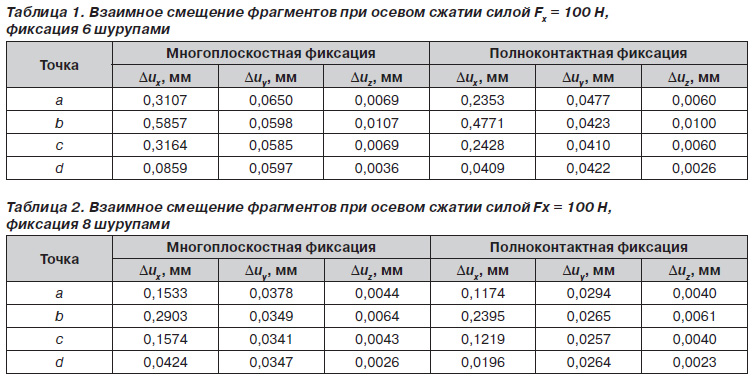
Другой вариант крепления фиксаторов отличается количеством используемых шурупов — по четыре с каждой стороны перелома с крепежными деталями (рис. 4).
Имеющиеся в настоящее время сведения о механических характеристиках костной ткани носят довольно отрывочный характер [8, 9, 13, 14], при этом неоспоримым фактом является значительный разброс экспериментальных данных и их существенная зависимость от возрастных особенностей и других факторов [1, 6, 7, 12]. На основе изучения упомянутых публикаций, а также [4, 10, 11] для большой берцовой кости приняты значения упругих свойств E =1 • 1010 Па и n = 0,36 в центральной части, а в зоне коленного и голеностопного суставов E = 9 • 109 Па, n = 0,38. Наибольшая неоднозначность характерна для свойств в области суставов. С учетом этого обстоятельства наряду с упомянутым выше значением модуля упругости принималось также E = 5 • 108 Па. Сопоставление полученных при этом результатов, как показано ниже, обнаружило их весьма незначительные различия, что позволяет считать влияние данной характеристики малосущественным. Предел прочности кости составляет 1,7 • 108 Па в центральной части и ориентировочно 2 • 107 Па в области суставов [4].
Обе рассматриваемые модели рассчитывались при трех вариантах силового воздействия, имитирующих физиологические нагрузки: осевом сжатии силой Fx, поперечном нагружении силой Fy (изгиб перпендикулярно плоскости планки) и действии поперечной силы Fz (изгиб в плоскости планки).
Некоторые результаты расчетов представлены далее в табличной форме и в виде иллюстраций. Для оценки подвижности зафиксированной кости в месте перелома рассматриваются значения компонент перемещений в характерных точках торцевых поверхностей фрагментов. Расположение упомянутых точек иллюстрирует рис. 5.
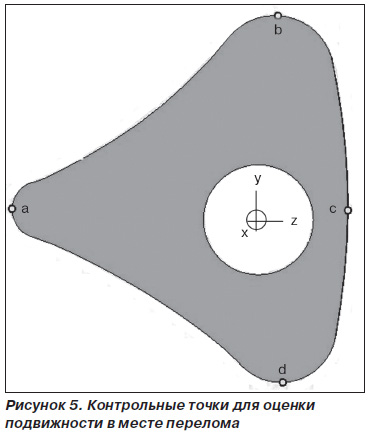
Относительные перемещения подсчитаны как разности соответствующих компонент для верхнего и нижнего торцов и характеризуют взаимное смещение фрагментов:
Dux = ux(верх) – ux(низ); Duу = uу(верх) – uу(низ); Duz = uz(верх) – uz(низ). (2)
Помимо перемещений существенное значение имеют данные о напряженном состоянии исследуемых объектов под действием приложенных нагрузок. В качестве обобщенной количественной характеристики уровня напряженного состояния обычно используется эквивалентное напряжение, при этом эквивалентность понимается в смысле попытки привести сложное напряженное состояние (когда отличны от нуля не менее двух компонент) к эквивалентному по опасности разрушения одноосному растяжению.
Наиболее употребительной среди подобных величин является интенсивность напряжений благодаря хорошему экспериментальному подтверждению. Интенсивность напряжений определяется по координатным компонентам в соответствии с формулой (3).
Уровень напряженного состояния всей конструкции и ее отдельных частей можно оценить по максимальным значениям интенсивности напряжений.
si = s2хх+s2уу+s2zz–sxxsyy–syyszz– syyszz+3(s2xy+s2xz+s2yz). (3)
Результаты и обсуждение
Ниже приведены численные результаты для упомянутого выше случая осевого сжатия Fx =100 Н. Табл. 1 и 2 содержат относительные перемещения фрагментов в характерных точках перелома при использовании шести и восьми крепежных шурупов соответственно.
Как видно из табл. 1, 2, многоплоскостная фиксация в данном случае обеспечивает большую подвижность фрагментов кости по сравнению с полноконтактной, что считается благоприятным фактором в ходе восстановительного периода. Микроподвижность фрагментов в определенной степени программирует тип их сращения. Наличие дополнительного шурупа с каждой стороны от перелома, естественно, увеличивает жесткость фиксации, что подтверждается сопоставлением данных табл. 1 и 2. То же наблюдается и для прочих вариантов нагружения.
Рис. 6 и 7 иллюстрируют напряженное состояние планки в виде полей интенсивностей напряжений для рассматриваемого случая нагружения при двух способах фиксации перелома шестью шурупами. Случай фиксации восемью шурупами показан на рис. 8 и 9.
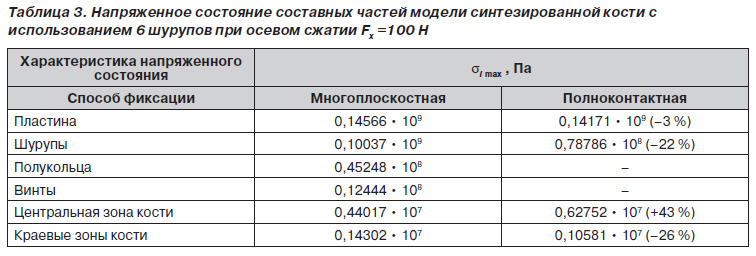
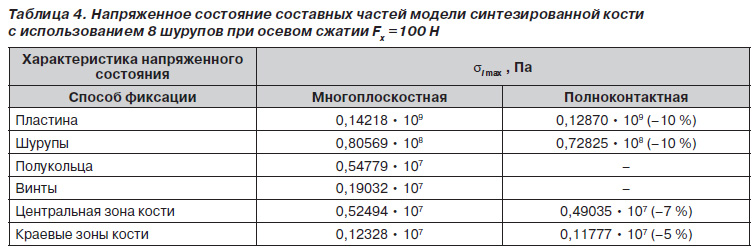
Максимальные значения интенсивности напряжений приведены в табл. 3 и 4.
Как видно, наиболее нагруженными частями конструкции являются пластина и шурупы, при этом в многоплоскостном фиксаторе уровень напряжений несколько выше, чем в полноконтактном. Центральная зона кости в случае фиксации 6 шурупами испытывает меньшие напряжения при многоплоскостном способе. Это подтверждает хорошие разгружающие возможности малоконтактного многоплоскостного фиксатора.
Вторым из возможных вариантов силового нагружения является изгиб перпендикулярно плоскости планки, т.е. в направлении ее наименьшей жесткости. (Это следует понимать как действие изгибающей нагрузки в упомянутом направлении; в действительности за счет эксцентриситета имеет место изгиб с кручением.) Величина поперечной силы Fy = 30 Н выбрана так, чтобы гарантировать отсутствие соприкосновения фрагментов кости.
Исследования показали, что большая взаимная подвижность фрагментов имеет место при многоплоскостной фиксации.
В то же время уровень напряженного состояния нагружения выше при полноконтактной фиксации, причем как для фиксатора, так и для кости. Исключение составляет центральная зона кости для варианта с 8 шурупами, что свидетельствует в пользу малоконтактного многоплоскостного фиксатора.
Действие поперечной нагрузки вдоль оси z соответствует изгибу конструкции в плоскости планки, т.е. в направлении ее наибольшей изгибной жесткости (здесь уместна та же оговорка, что и для изгиба из плоскости планки). Это значит, что отсутствие соприкосновения фрагментов кости возможно при гораздо большей нагрузке, чем в предыдущем случае. В связи с этим для сравнительного анализа двух вариантов фиксации выбрано значение силы Fz = 100 Н.
Исследования показали, что большая взаимная подвижность фрагментов имеет место в основном при многоплоскостной фиксации, за исключением относительных смещений вдоль оси x точек b и d. Они расположены вблизи малоконтактной пластины.
Следует отметить, что уровень напряженного состояния фиксатора и кости был выше при многоплоскостной фиксации для варианта 6 крепежных шурупов. Вариант из 8 шурупами давал полностью противоположный результат. Это говорит о преимуществе малоконтактного многоплоскостного фиксатора.
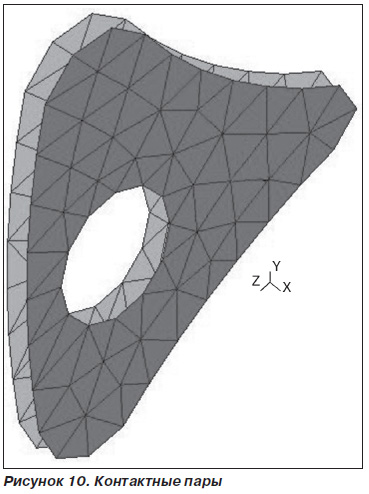
Описанные выше результаты расчетов соответствуют действию относительно небольших силовых нагрузок, при которых фрагменты кости не вступают в соприкосновение между собой в месте перелома. В таком случае задача об упругом статическом деформировании конструкции, состоящей из двух фрагментов кости и фиксатора вместе с крепежными деталями, является линейной и поэтому решается сравнительно просто. С другой стороны, исследование обозначенной в данном разделе проблемы нельзя признать полным без рассмотрения возможного соприкосновения между торцевыми поверхностями фрагментов под действием внешней нагрузки. Это приводит к необходимости постановки и решения контактной задачи. Сложность контактной задачи обусловлена ее конструктивной нелинейностью, поскольку зоны контакта взаимодействующих тел и распределения в них реакций заранее неизвестны и должны быть найдены в результате решения. Конечноэлементный анализ в этом случае осуществляется с использованием дополнительных специализированных конечных элементов, имитирующих контактное взаимодействие. Эти элементы создаются на обеих взаимодействующих поверхностях и образуют контактные пары. Для численного решения нелинейной контактной задачи применяется итерационная процедура расширенного метода множителей Лагранжа, представляющего собой модификацию метода штрафных функций [3].
Контактные пары, созданные на торцевых поверхностях фрагментов в месте перелома, показаны на рис. 10, причем для вариантов многоплоскостной и полноконтактной фиксации они полностью идентичны.
Ниже приведены результаты решения контактной задачи для случая осевого сжатия силой Fx = 800 Н. Найденные в результате решения поля контактных давлений (Па) при двух способах фиксации оказались весьма схожими.
Полученные результаты показали, что большая взаимная подвижность фрагментов вдоль осей x и y имеет место в основном при многоплоскостной фиксации; в направлении z относительные смещения сравнительно невелики и мало отличаются для двух моделей.
Относительно интенсивности напряжений пластин исследования показали, что многоплоскостная фиксация обеспечивает более равномерное распределение нагрузки в фиксаторе при меньшем уровне напряжений в пластине, что свидетельствует о ее биомеханическом преимуществе.
С точки зрения напряженно-деформированного состояния наиболее неблагоприятным случаем внешнего силового воздействия является изгиб поперечной нагрузкой перпендикулярно плоскости планки. Усилие величиной Fy = 100 Н вызывает соприкосновение фрагментов сломанной кости.
Относительные перемещения характерных точек на торцевых поверхностях фрагментов показали, что бόльшая взаимная подвижность фрагментов вдоль осей x и z имеет место в основном при многоплоскостной фиксации; в направлении y такая фиксация обнаруживает относительно бόльшую жесткость в случае использования шести шурупов.
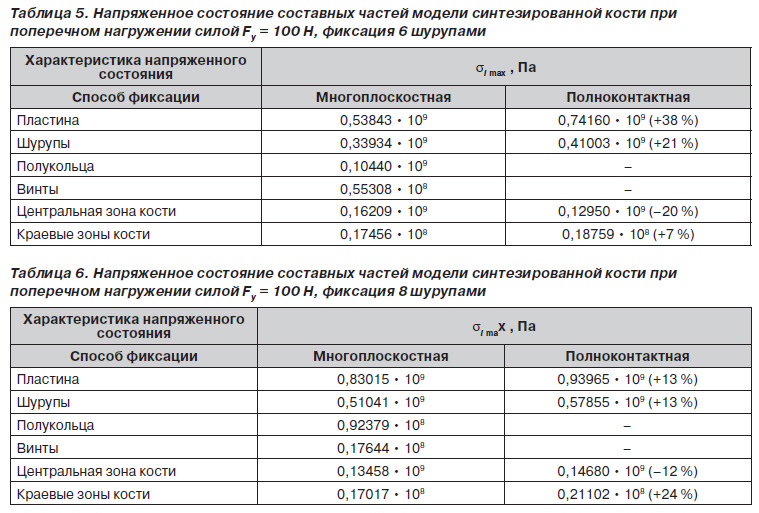
Интересные данные получены о состоянии максимальных напряжений шурупов, полуколец и пластин при разных способах фиксации (табл. 5 и 6).
Как видно из табл. 5, 6, в рассматриваемом случае при полноконтактной фиксации пластина и крепежные детали подвержены значительно большей нагрузке по сравнению с многоплоскостной фиксацией. Центральная зона кости испытывает относительно меньшие напряжения. Все это свидетельствует о большом биомеханическом преимуществе малоконтактного многоплоскостного остеосинтеза.
Таким образом, теоретически изучена реакция скрепленной фиксатором большеберцовой кости на действие физиологических нагрузок путем статического анализа четырех расчетных моделей. Рассмотрено в общей сложности пять вариантов нагружения, в том числе два — с учетом контактного взаимодействия фрагментов.
Обобщая результаты сравнительных теоретических исследований, следует отметить, что многоплоскостной фиксатор в подавляющем большинстве случаев обнаруживает преимущество перед традиционным полноконтактным в отношении микроподвижности фрагментов кости.
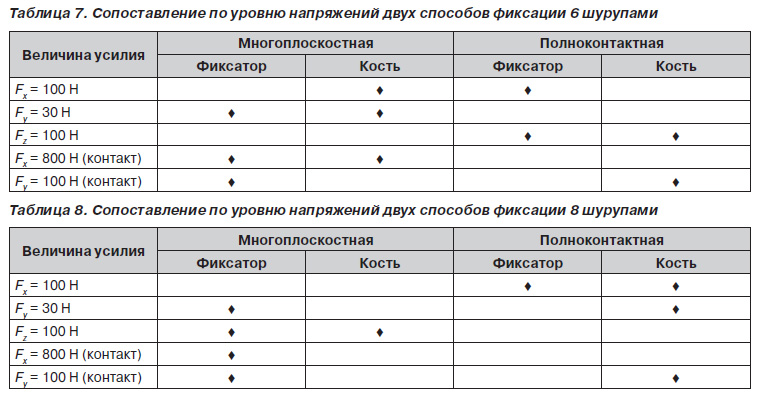
Немаловажным аспектом является также преимущество многоплоскостной фиксации, особенно при лизисе кости и нагрузке: исключается переход микроподвижности фрагментов в макроперемещение. Полноконтактная одноплоскостная фиксация не препятствует такому переходу. Наглядное представление о соотношении двух способов фиксации дают сравнительные таблицы 7 и 8, в которых символ «¨» означает предпочтительный вариант, т.е. меньший уровень напряжений.
Несмотря на отсутствие однозначного соотношения, некоторое преимущество, особенно с позиций напряженного состояния фиксатора, имеет многоплоскостной способ.
Согласно полученным результатам, наибольший уровень напряженного состояния в планке фиксатора (а также в полукольцах при многоплоскостной фиксации) наблюдается вблизи контуров свободных отверстий. Поэтому с целью повышения надежности фиксатора и уменьшения опасности поломки представляется целесообразным иметь в наличии пластины без 1–2 отверстий в центре для возможности подбора необходимого варианта.
Исследования показали, что такие пластины обеспечивают более однородное напряженное состояние в центральной части планки, при этом снижается уровень наибольших напряжений.
Заключение
Таким образом, представленные исследования показали, что малоконтактная многоплоскостная фиксация имеет значительно больше преимуществ в сравнении с одноплоскостной полноконтактной, поскольку исключает переход микроподвижности фрагментов в макроперемещение при нагрузке, а также исключает давление пластины на кость.
Важным обстоятельством в практическом применении является возможность широкого маневра, который обеспечивает многоплоскостная фиксация для адаптации к конкретному клиническому случаю за счет варьирования конструктивного решения путем изменения положения и количества полуколец и шурупов. Кроме этого, недостатком полноконтактного фиксатора следует признать необходимость, как правило, большего количества шурупов для его установки, что дополнительно травмирует кость. Все это свидетельствует о перспективности применения малоконтактных многоплоскостных фиксаторов.
- Березовский В.А. Биофизические характеристики тканей человека / В.А. Березовский, Н.П. Колотилов. — К.: Наукова думка, 1990. — 224 с.
- Метод конечных элементов / Под ред. П.М. Варвака. — К.: Вища школа, 1981. — 176 с.
- Пантелеев А.В. Методы оптимизации в примерах и задачах: Учеб. пособие / А.В. Пантелеев, Т.А. Летова — М.: Высшая школа, 2002. — 544 с.
- Писаренко Г.С. Деформирование и прочность материалов при сложном напряженном состоянии / Г.С. Писаренко, А.А. Лебедев. — К.: Наукова думка, 1976. — 415 с.
- Сегерлинд Л. Применение метода конечных элементов / Л. Сегерлинд. — М.: Мир, 1979. — 392 с.
- Elastic modulus and hardness of cortical and trabecular bovine bone measured by nanoindentation / [Wang X.J., Chen X.B., Hodgson Peter and Wen Cui`e] // Transactions of Nonferrous Metals Society of China. — 2006. — Vol. 16 (2). — P. 744-748.
- http://www.doitpoms.ac.uk/tlplib/bones/bone_mechanical.php
- Katsamanis F. Determination of mechanical properties of human femoral cortical bone by the Hopkinson bar stress technique / F. Katsamanis, D.D. Raftopoulos // J. Biomech. — 1990. — Vol. 23 (11). — P. 1173-1184.
- Maquet P.J. Biomechanics of the knee / P.J. Maquet. — Berlin: Springer-Verlag, 1984. — 306 p.
- Reilly D.T. The elastic and ultimate properties of compact bone tissue / D.T. Reilly, A.H. Burstein // J. Biomech. — 1975. — Vol. 8. — P. 393-405.
- Rho J.Y. Young’s modulus of trabecular and cortical bone material: ultrasonic and microtensile measurements / J.Y. Rho, R.B. Ashman, C.H. Turner // J. Biomech. — 1993. — Vol. 26 (2). — P. 111-119.
- The elastic moduli of human subchondral, trabecular, and cortical bone tissue and the size-dependency of cortical bone modulus / [Choi K., Kuhn J.L., Ciarelli M.J., Goldstein S.A.] // J. Biomech. — 1990. — Vol. 23 (11). — P. 1103-1113.
- Weiner S. Lamellar Bone: Structure — Function Relations / S. Weiner, W. Traub, H.D. Wagner // J. Struct. Biology. — 1999. — Vol. 126. — P. 241-255.
- Yoon H.S. Ultrasonic wave propagation in human cortical bone. II Measurements of elastic properties and microhardness / H.S. Yoon, J.L. Katz // J. Biomech. — 1976. — Vol. 9. — P. 459-464.