Резюме
Актуальність. Математичне моделювання корекції сколіотичних деформацій хребта дозволяє без хірургічного втручання провести аналіз ефективності різних методів лікування в декількох варіантах. При дослідженні тракційних способів лікування застосовувалися переважно експериментальні методи досліджень. Мета: дослідити напружено-деформований стан моделей хребта з різним ступенем сколіотичної деформації при задньому спондилодезі. Матеріали та методи. Моделювали деформації хребта 40°, 70° і 100° при задньому спондилодезі хребців Th1-Th12. Використовували навантаження величиною 300 Н. Результати. При деформації 40° найбільш напруженими є ділянки вигину хребта у фронтальній площині. Для верхніх хребців Th1-Th4 спостерігається більш рівномірний розподіл напруження по тілу хребця. Для блоку хребців Th5-Th10 більш напруженою є увігнута сторона тіл хребців. У грудному відділі хребта найбільш напруженими є хребці Th2 і Th5. Основне навантаження несе фіксуюча конструкція, у якій рівень напруженого стану значно вищий, ніж у кісткових структурах хребців. У задньому опорному комплексі хребців ділянки концентрації напруження розташовані у місцях входу фіксуючих гвинтів у кістку. Збільшення величини сколіотичної деформації хребта до 70° викликає збільшення рівня напруження в усіх елементах моделі, за винятком хребців Th9-Th10. При деформації 100° у задньому опорному комплексі хребців ділянки концентрації напруження розташовані у місцях входу фіксуючих гвинтів у кістку. Рівень напруження 116,0 МПа перевищує межу міцності кортикального шару кісткової тканини хребта, що може призвести до мікроушкоджень кісткової тканини та розхитування гвинтів. Висновки. При всіх величинах сколіотичної деформації хребта найбільш напруженими є хребці Th4 та Th5. Зменшення ступеня деформації значно впливає на напружено-деформований стан хребетного стовпа. У тілі хребця Th4 рівень напруження при деформації 100° більш ніж удвічі вищий, ніж при деформації 70°, та більш ніж у 4 рази, ніж при деформації 40°. У тілі хребця Th5 рівень напруження при деформації 70° в 1,5 раза менше, ніж при деформації 100°, а при деформації 40° — менше в 3 рази. Рівень напруження в тілах хребців Th1-Th5 вищий, ніж у Th6-Th12. У задньому опорному комплексі в місцях входу гвинтів у кістку максимальне значення напруження при деформації 40° дорівнює 34,0 МПа, що не є критичним для кісткової тканини. При деформації 70° значення напруження дорівнює 85,0 МПа, що може перевищувати межу міцності для кортикальної кістки і призводити до мікроруйнування кісткової тканини в ділянці контакту «гвинт — кістка». При деформації 100° напруження дорівнює 116,0 МПа, що перевищує межу міцності для кортикальної кістки і може призвести до мікроруйнування в ділянці контакту «гвинт — кістка».
Background. Mathematical modeling of the correction of scoliotic deformities of the spine makes it possible to analyze the effectiveness of various methods of treatment without surgical intervention. In the study of traction, mainly experimental methods were used. The purpose was to investigate the stress-strain state of the spine models with varying degrees of scoliotic deformity during posterior spinal fusion. Materials and methods. Deformities of the spine of 40, 70 and 100° were modeled, with posterior spondylodesis of the Th1-Th12 vertebrae. A load of 300 N was used. Results. With a deformity of 40°, the most stressed are the areas of frontal plane curve. For the upper vertebrae Th1-Th4, a more even distribution of stress over the vertebral body is observed. For Th5-Th10 vertebrae, the concave side of the vertebral bodies is more stressed. In the thoracic spine, the more stressed vertebrae are Th2 and Th5. The main load is borne by the fixing structure, in which the level of stress is significantly higher than in the bone structures of the vertebrae. In the posterior supporting complex of the vertebrae, the stress concentration areas are located at the points where fixing screws enter the bone. An increase in the magnitude of the scoliotic deformity of the spine up to 70° causes an increase in the level of stresses in all elements of the model, with the exception of Th9-Th10 vertebrae. With a deformity of 100° in the posterior supporting complex of the vertebrae, the stress concentration areas are located at the points where fixing screws enter the bone. The stress level of 116.0 MPa exceeds the ultimate strength of the cortical layer of the bone tissue of the spine, which can lead to microdamage of the bone tissue and loosening of the screws. Conclusions. For all values of scoliotic deformity of the spine, the most stressed are Th4 and Th5 vertebrae. A decrease in the degree of deformity has a significant effect on the stress-strain state of the spinal column. In the Th4 vertebral body, the level of stresses with a deformity of 100° is more than twice as high as with a deformity of 70°, and more than 4 times higher than with a deformity of 40°. In the body of the Th5 vertebra, the stress level with a deformity of 70° is 1.5 times less than with a deformity of 100°, and with a deformity of 40°, it is 3 times less. The level of stress in the Th1-Th5 vertebral bodies is higher than that of Th6-Th12. In the posterior supporting complex, at the points where screws enter the bone, the maximum stress value at a deformity of 40° is 34.0 MPa, which is not critical for the bone tissue. With a deformity of 70°, the stresses are 85.0 MPa, which can exceed the ultimate strength for the cortical bone and lead to microdestruction of the bone tissue in the screw-bone contact area. With a deformity of 100°, the stresses are equal to 116.0 MPa, which exceeds the ultimate strength for the cortical bone and can lead to microfracture in the screw-bone contact area.
Вступ
Математичне моделювання корекції сколіотичних деформацій хребта дозволяє провести аналіз ефективності різних методів лікування в декількох варіантах. З кінця минулого сторіччя найбільше поширення отримало моделювання біомеханічних систем методом скінченних елементів (МСЕ), який у сполученні з експериментальними методами дозволяє отримати вірогідні результати. Одна з перших простих моделей із використанням МСЕ для моделювання коригуючих зусиль при хірургічному лікуванні сколіозу була наведена в роботі D.N. Ghista et al. [1].
Подальший розвиток моделювання методів лікування сколіозу дозволив побудувати геометрично та фізично складніші скінченно-елементні моделі. Так, у роботі N.M. Lalonde et al. [2] проводився аналіз складної тривимірної моделі хребта в передопераційному положенні на боці, що моделює зміни хребта внаслідок переходу з положення стоячи. Скінченно-елементний аналіз проводився переважно для різних моделей хірургічного втручання при лікуванні сколіозу [3–9].
При дослідженні тракційних способів лікування застосовувалися переважно експериментальні методи досліджень. Більша кількість робіт присвячена визначенню кількості гвинтів галотракційної конструкції [10] або їх оптимального розташування [11, 12].
Мета: дослідити напружено-деформований стан моделей хребта з різним ступенем сколіотичної деформації при задньому спондилодезі.
Матеріали та методи
При побудові розрахункової моделі за основу були взяті геометричні моделі різних ділянок хребта, розроблені в лабораторії біомеханіки ДУ «Інститут патології хребта та суглобів ім. проф. М.І. Ситенка НАМН України» [8, 9], в основу будови яких закладена методика створення моделі по геометричним перетинам, отриманим із томографічних знімків.
Згідно з метою дослідження в модель були внесені такі зміни: деформація хребта 40°, 70° і 100°, додана модель стрижневого апарата для заднього спондилодезу хребців Th1-Th12. Зовнішній вигляд моделей наведений на рис. 1.
У цьому дослідженні матеріал вважали однорідним та ізотропним. При виборі властивостей кісткових структур використовували дані, що найчастіше зустрічаються в літературі [13, 14]. Характеристики модуля пружності Е (модуль Юнга), коефіцієнта Пуассона ν наведені в табл. 1.
При моделюванні розглядали двохопорне стояння. Використовували навантаження величиною 300 Н, що відповідає половині ваги тіла людини. Розподіл навантаження вздовж хребта задано відповідно до досліджень [15, 16]. Нижня площина тіла хребця L5 жорстко зафіксована. Схема навантаження моделі наведена на рис. 2.
Побудова геометричної моделі проводилася з використанням програми SolidWorks [17]. Для вирішення поставленого завдання був використаний метод скінченних елементів [18].
Як оцінка напруженого стану обране напруження за Мізесом як найбільш інформативний вид загального напруженого стану.
Результати
На першому етапі роботи вивчали напружено-деформований стан (НДС) моделі при наявності величини сколіотичної деформації 40°. Картина розподілу напруження в моделі наведена на рис. 3.
Аналіз НДС моделі показав, що найнапруженішими ділянками є блоки хребців у місцях найбільшого викривлення хребетного стовпа. Так, для верхніх хребців Th1-Th4 рівень напруженого стану вищий у хребцях Th1, Th2 і досягає величини 9,6 МПа. У середній частині грудного відділу хребта Th5-Th8 підвищений рівень напруження спостерігається у хребці Th5 — 9,5 МПа, а в нижній частині — у хребцях Th9-Th10, де значення напруження сягають величини 4,8 МПа. Значну частину навантаження несе апарат зовнішньої фіксації: так, на фіксуючих гвинтах хребця Th8 спостерігається найвищий рівень напруження — 250,0 МПа. У задньому опорному комплексі в місці входу гвинтів у кістку у хребцях Th5-Th9 величина напруження спостерігається на рівні 34,0 МПа. У блоці хребців L1-L5 рівень напруженого стану нижчий і не перевищує 2,5 МПа.
Проведений розрахунок дозволяє зробити такі висновки:
1) найбільш напруженими ділянками моделі є ділянки вигину хребта у фронтальній площині;
2) для верхніх хребців Th1-Th4 спостерігається більш рівномірний розподіл напруження по тілу хребця;
3) для блоку хребців Th5-Th10 найбільш напруженою є ліва (увігнута) сторона тіл хребців;
4) у грудному відділі хребта найбільш напруженими є хребці Th2 і Th5;
5) основне навантаження несе фіксуюча конструкція, у якій рівень напруженого стану значно вищий, ніж у кісткових структурах хребців;
6) у задньому опорному комплексі хребців грудного відділу ділянки концентрації напруження розташовані у місцях входу фіксуючих гвинтів у кістку;
7) рівень напруженого стану як у кісткових структурах, так і в фіксуючій конструкції не перевищує межі міцності матеріалів.
На другому етапі роботи вивчали напружено-деформований стан моделі хребта із заднім спондилодезом при величині сколіотичної деформації 70°. Картину розподілу напруження в моделі можна спостерігати на рис. 4.
Аналіз НДС моделі показав, що найбільш напруженими ділянками є блоки хребців у місцях найбільшого викривлення хребетного стовпа, як і в моделі з 40° деформацією. Так, для верхніх хребців Th1-Th4 рівень напруженого стану є найвищим у хребцях Th1, Th2 і досягає величини 15,4 МПа (9,6 МПа для моделі з 40° деформацією). У середній частині грудного відділу хребта Th5-Th8 найвищий рівень напруження спостерігається у хребці Th5 — 21,3 МПа (9,5 МПа для моделі з 40° деформацією). У нижній частині у хребцях Th9-Th10 значення напруження практично не змінилося і досягає величини 4,3 МПа (4,8 МПа для моделі з 40° деформацією). Значну частину навантаження бере на себе апарат зовнішньої фіксації. Так, у фіксуючих гвинтах у хребці Th7 спостерігається найвищий рівень напруження — 320,0 МПа (250,0 МПа для моделі з 40° деформацією). У задньому опорному комплексі на місці входу гвинтів у кістку для хребців Th5-Th9 рівень напруження досягає величини 85,0 МПа (34,0 МПа для моделі з 40° деформацією). У блоці хребців L1-L5 найвищий рівень напруження більш низький і не перевищує 4,7 МПа (2,5 МПа для моделі з 40° деформацією).
Таким чином, проведений розрахунок дозволяє стверджувати, що збільшення величини сколіотичної деформації хребта викликає збільшення рівня напруження в усіх елементах моделі, за винятком хребців Th9-Th10.
На останньому етапі роботи вивчали напружено-деформований стан моделі хребта із заднім спондилодезом при величині сколіотичної деформації 100°. На рис. 5 наведена картина розподілу напруження в зазначеній моделі.
Аналіз НДС моделі показав, що найнапруженішими ділянками є блоки хребців у місцях найбільшого викривлення хребетного стовпа, як і в попередніх моделях. Так, для вершинних хребців Th1-Th4 рівень напруженого стану найвищий у хребцях Th1, Th2 і досягає величини 17,1 МПа (15,4 МПа для моделі з 70° деформацією). У середній частині грудного відділу хребта Th5-Th8 підвищений рівень напруження спостерігається у хребці Th5 — 31,8 МПа (21,3 МПа для моделі з 70° деформацією). У нижній частині у хребцях Th9-Th10 значення напруження практично не змінилося і досягає величини 4,2 МПа (4,3 МПа для моделі з 70° деформацією). Значну частину навантаження бере на себе апарат зовнішньої фіксації: так, на фіксуючих гвинтах у хребці Th7 рівень напруженого стану дорівнює 380,0 МПа (320,0 МПа для моделі з 70° деформацією). У задньому опорному комплексі на місці входу гвинтів у кістку для хребців Th5-Th9 рівень напруженого стану досягає величини 116,0 МПа (85,0 МПа для моделі з 70° деформацією). У блоці хребців L1-L5 найбільший рівень напруженого стану більш низький і не перевищує 6,3 МПа (4,7 МПа для моделі з 70° деформацією).
/22.jpg)
Проведений розрахунок дозволяє стверджувати, що збільшення величини сколіотичної деформації хребта викликає зростання рівня напруження в усіх елементах моделі. Виняток, як і раніше, становлять хребці Th9-Th10.
У задньому опорному комплексі хребців грудного відділу ділянки концентрації напруження розташовані у місцях входу фіксуючих гвинтів у кістку. Рівень напруженого стану для розрахункової моделі 116,0 МПа перевищує межу міцності кортикального шару кісткової тканини хребта [11], що може призвести до мікроушкоджень кісткової тканини та розхитування гвинтів. Рівень напруженого стану в інших елементах моделі визначається у межах міцності матеріалів.
Дані про максимальні величини напруження в кісткових елементах моделей при різних величинах сколіотичної деформації наведені в табл. 2.
Наочне уявлення про величину напруження у грудному відділі хребта із заднім спондилодезом при різних величинах сколіотичної деформації можна отримати за допомогою діаграми, яка наведена на рис. 6.
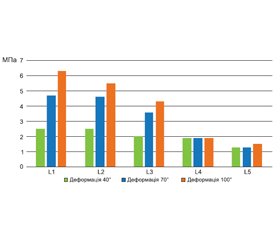
Для порівняння величини напруження у хребцях поперекового відділу хребта із заднім спондилодезом при різних величинах сколіотичної деформації побудована діаграма, яка наведена на рис. 7.
Висновки
1. У нашому дослідженні при всіх величинах сколіотичної деформації хребта найбільш напруженими є хребці Th4 та Th5.
2. Зменшення ступеня деформації значно впливає на напружено-деформований стан хребетного стовпа.
3. У тілі хребця Th4 рівень напруження при деформації 100° більш ніж удвічі вищий порівняно з моделлю хребта з деформацією 70° та більш ніж у 4 рази — порівняно з моделлю хребта з деформацією 40°.
4. У тілі хребця Th5 рівень напруженого стану при деформації 70° менше в 1,5 раза, ніж у моделі хребта з деформацією 100°, а при деформації 40° — менше в 3 рази.
5. Під час дослідження доведено, що рівень напруженого стану в тілах хребців (Th1-Th5 — верхній рівень полісегментарної інструментації) вищий, ніж у нижчерозташованих (Th6-Th12 — середній і нижній рівні інструментації).
6. У задньому опорному комплексі в місцях входу гвинтів у кістку (найбільш напружених хребців) максимальне значення напруження при деформації 40° дорівнює 34,0 МПа, що не є критичним для кісткової тканини з точки зору міцності (межа міцності для кортикальної кістки, за різними джерелами, становить від 70,0 до 120,0 МПа).
7. У задньому опорному комплексі в місцях входу гвинтів у кістку (найбільш напружених хребців) максимальне значення напруження при деформації 70° дорівнює 85,0 МПа, що може перевищувати межу міцності для кортикальної кістки і призводити до мікроруйнування кісткової тканини в ділянці контакту «гвинт — кістка».
8. У задньому опорному комплексі в місцях входу гвинтів у кістку (найбільш напружених хребців) максимальне значення напруження при деформації 100° дорівнює 116,0 МПа, що перевищує межу міцності для кортикальної кістки і може призвести до мікроруйнування в ділянці контакту «гвинт — кістка».
Конфлікт інтересів. Автори заявляють про відсутність конфлікту інтересів і власної фінансової зацікавленості при підготовці даної статті.
Отримано/Received 10.11.2021
Рецензовано/Revised 26.11.2021
Прийнято до друку/Accepted 02.12.2021
Список литературы
1. Ghista D.N., Viviani G.R., Subbaraj K. et al. Biomechanical basis of optimal scoliosis surgical-correction. J. Biomech. 1988. № 21(2). P. 77-88. DOI: 10.1016/0021-9290(88)90001-2.
2. Lalonde N.M., Villemure I., Pannetier R. et al. Biomechanical modeling of the lateral decubitus posture during corrective scoliosis surgery. Clin. Biomech. 2010. № 25. P. 510-516. DOI: 10.1016/j.clinbiomech.2010.03.009.
3. Lafage V., Dubousset J., Lavaste F., Skalli W. Finite element simulation of various strategies for CD correction. Stud. Health Technol. Inform. 2002. № 91. Р. 428-432.
4. Lafon Y., Steib J.P., Skalli W. Intraoperative three dimensional correction during in situ contouring surgery by using a numerical model. Spine (Phila Pa 1976). 2010. № 35. P. 453-459. DOI: 10.1097/BRS.0b013e3181b8eaca.
5. Salmingo R., Tadano S., Fujisaki K. et al. Corrective force analysis for scoliosis from implant rod deformation. Clin. Biomech. (Bristol, Avon). 2012. № 27. P. 545-550. DOI: 10.1016/j.clinbiomech.2012.01.004.
6. Little J.P., Izatt M.T., Labrom R.D., Askin G.N., Adam C.J. An FE investigation simulating intra-operative corrective forces applied to correct scoliosis deformity. Scoliosis. 2013 May 16. № 8(1). Р. 9. DOI: 10.1186/1748-7161-8-9.
7. Петренко Д.Є., Мезенцев А.О., Яресько О.В. Аналіз напружено-деформованого стану грудного та поперекового відділів хребта після фіксації вентральним імплантатом. Літопис травматології та ортопедії. 2013. № 3–4. С. 25-29.
8. Головаха M.Л., Тяжелов А.A., Летучая Н.П., Суббота И.A., Карпинский M.Ю. Биомеханические аспекты экспериментального исследования функционального лечения С-образной сколиотической деформации позвоночника. Травма. 2019. Т. 20. № 3. С. 32-41. DOI: 10.22141/1608-1706.3.20.2019.172091.
9. Головаха М.Л., Тяжелов А.А., Летучая Н.П., Суббота И.А., Карпинский М.Ю. Биомеханические аспекты экспериментального исследования функционального лечения S-образной сколиотической деформации позвоночника. Травма. 2018. Т. 19. № 1. C. 58-68. DOI: 10.22141/1608-1706.1.19.2018.126661.
10. Kimsal J., Khraishi T. Experimental investigation of halo-gravity traction for paediatric spinal deformity correction. Int. J. Experimental and Computational Biomechanics. 2009. Vol. 1. № 2. P. 204-213. DOI: 10.1504/IJECB.2009.029197.
11. Semmelink K., Hekman E.E.G, van Griethuysen M., Bosma J., Swaan A., Kruyt M.C. Halo pin positioning in the temporal bone; parameters for safe halo gravity traction. Spine Deform. 2021 Jan. № 9(1). Р. 255-261. DOI: 10.1007/s43390-020-00194-2.
12. Fialho J. A biomechanical model for the idiopathic scoliosis using robotic traction devices. International Conference on Mathematical Modelling in Physical Sciences IOP Conf. Series: Journal of Physics. Conf. Series 1141. 2018. 012022. DOI: 10.1088/1742-6596/1141/1/012022.
13. Kong W.Z., Goel V.K. Ability of the Finite Element Mo-dels to Predict Response of the Human Spine to Sinusoidal Vertical Vibration. Spine. 2003. Vol. 28. № 17. Р. 1961-1967. DOI: 10.1097/01.BRS.0000083236.33361.C5.
14. Vidal-Lesso A., Ledesma-Orozco E., Daza-Benítez L., Lesso-Arroyo R. Mechanical Characterization of Femoral Cartilage Under Unicompartimental Osteoarthritis. Ingeniería mecánica tecnología y desarrollo. 2014. Vol. 4. № 6. Р. 239-246.
15. Shirazi-Adl A., El-Rich M., Pop D.G., Parnianpour M. Spinal muscle forces, internal loads and stability in standing under various postures and loads — application of kinematics-based algorithm. Eur. Spine J. 2005. № 14. Р. 381-392. DOI: 10.1007/s00586-004-0779-0.
16. Мезенцев А.А., Чекрижев Д.О., Карпінський М.Ю., Субота І.А. Біомеханічне моделювання умов навантаження хребта при лікуванні сколіозу методом корсетотерапії. Медицина и... 2005. № 1. С. 45-49.
17. Kurowski P.M. Engineering Analysis with SolidWorks Simulation. 2012. Published April 11, 2012. 475 р.
18. Zienkiewicz O.C., Taylor R.L. The Finite Element Method for Solid and Structural Mechanics. Sixth ed. Butterworth-Heinemann, 2005. 736 p.

/20.jpg)
/21.jpg)
/22.jpg)
/23.jpg)