Резюме
Актуальність. Вибухові переломи тіл нижньогрудного та поперекового відділів хребта є найбільш розповсюдженими серед усіх пошкоджень та становлять, за даними різних авторів, від 20 до 40 % усіх пошкоджень хребта. Мета: вивчити біомеханічні характеристики кіфотичної деформації в залежності від прикладеного осьового стискаючого навантаження, що діє вздовж усього хребта, та ступеня пошкодження хребтових структур. Матеріали та методи. Біомеханічна фізична модель вибухового перелому тіла Th12 хребця, що була виконана на анатомічних препаратах блоків хребтових сегментів тварини (свині). У першій групі збережені кісткові і зв’язкові структури. У другій зруйновано до 50 % тіла хребця. У третій зруйновано усе тіло (100 %) та два суміжних диска. У четвертій зруйновано 100 % тіла, диски, дуги, зв’язки і суглоби. Результати. У залежності від ступеня руйнування хребтово-рухового сегмента Тh12 загальний модуль пружності моделі зменшується за рахунок випадання з опорної функції елементів сегмента. Максимальний модуль пружності має модель із незруйнованими структурами при всіх видах навантажень. Зменшення модуля пружності до граничних величин досягалося в зразках зі зруйнованим тілом хребця, диска, задніх структур при середніх та максимальних навантаженнях. Даний вид моделі є максимально нестабільним, з відсутнім модулем пружності. Висновки. При збільшенні обсягу руйнувань хребтово-рухового сегмента Th12 величина осьового стискання моделі під дією стискаючих навантажень статистично достовірно збільшується при всіх величинах стискаючої сили. Залежно від ступеня руйнування хребтово-рухового сегмента Th12 модуль загальної деформації моделі зменшується. Порушення міцності моделі відбулося на етапі руйнування 50 % тіла хребця та вищерозміщеного міжхребцевого диска при інтенсивності навантаження 100 Н. Зі збільшенням ступеня руйнування зразок втрачає здатність опиратися зростаючим навантаженням, що підтверджується зменшенням модуля загальної деформації досліджуваних зразків.
Актуальность. Взрывные переломы тел нижнегрудного и поясничного отделов позвоночника являются наиболее распространенными среди всех повреждений и составляют, по данным разных авторов, от 20 до 40 % всех повреждений позвоночника. Цель: изучить биомеханические характеристики кифотической деформации, развивающейся под воздействием осевой сжимающей нагрузки, действующей вдоль всего позвоночника, в зависимости от степени повреждения позвоночных сегментов. Материалы и методы. Физическая модель взрывного перелома тела Th12 позвонка, которая была выполнена на анатомических препаратах блоков позвоночных сегментов животного (свинья). В первой группе сохранены костные и связочные структуры. Во второй разрушено до 50 % тела позвонка. В третьей разрушено все тело (100 %) и два смежных диска. В четвертой разрушено тело (100 %), диски, дуги, связки и суставы. Результаты. В зависимости от степени разрушения позвоночно-двигательного сегмента Th12 общий модуль упругости модели снижается за счет выпадения из опорной функции элементов сегмента. Максимальным модулем упругости обладает биомеханическая модель с неразрушенными структурами при всех видах нагрузок. Снижение модуля упругости до предельных величин достигалось в образцах с разрушенным телом позвонка, дисков, задних структур при средних и максимальных нагрузках. Данный вид модели является максимально нестабильным, с отсутствием модуля упругости. Выводы. При увеличении объема разрушений позвоночно-двигательного сегмента Th12 величина осевого сжатия модели под действием сжимающих нагрузок статистически достоверно увеличивается при всех величинах сжимающей силы. В зависимости от степени разрушения позвоночно-двигательного сегмента Th12 модуль общей деформации модели снижается за счет выпадения из опорной функции элементов сегмента. В зависимости от степени разрушения и величины прилагаемой нагрузки встречаются как упругие, так и пластические виды деформации. Нарушение прочности модели произошло на этапе разрушения 50 % тела позвонка и вышележащего межпозвоночного диска при интенсивности нагружения 100 Н. С увеличением степени разрушения образец теряет способность противостоять возрастающим нагрузкам, что подтверждается уменьшением модуля общей деформации исследуемых образцов.
Background. According to various authors, burst fractures of lower thoracic and lumbar spine are the most common among the whole number of injuries and take 20–40 % of all spine traumas. The purpose of the study was to explore the biomechanical characteristics of kyphosis that develops under the influence of the axial compressive load along the entire spine, depending on the degree of damage to the spinal segment. Materials and methods. Physical model of burst fracture of Th12 vertebra was realized on anatomic preparations of blocks of vertebral segments of the animal (pig). In the first group, bone and ligamentous structures were saved. In the second group, up to 50 % of the vertebral body was destroyed. In the third group — all the body and two adjacent spinal disks. In the forth group — 100 % of the body, disks, archs, ligaments and joints. Results. Depending on the degree of destruction of the functional spinal unit Th12, general elastic modulus of the model is reduced. It happens due to the loss of the support function of the elements of the segment. The biomechanical model with nondestructive structures for all kinds of loads has the maximum elastic modulus. With destruction of the anatomical structures and with increasing stresses, the elastic modulus decreases progressively. Reduction of the elastic modulus to the limit values was achieved by samples with destroyed vertebral body, disks, posterior structures at medium and maximum loads. This type of model is the most unstable, with no elastic modulus. Samples with damage to the vertebral body by 50 % and the disk and samples with 100 % damage of the vertebral body and 2 disks have a certain level of elastic modulus that depends on the load and degree of destruction, i.e. they are stable samples with regard to the value of the primary deformation. Conclusions. By increasing the amount of destruction of the spinal motion segment Th12, the value of axial compression of the model under compressive load was significantly increased for all values of the compressive force. Depending on the degree of destruction of the spinal motion segment Th12, the modulus of total deformation of the model is reduced due to loss of the support function of the segment elements. Depending on the degree of damage and the applied load values, there are both elastic and plastic deformation types. Violation of the strength of the model was at the stage of 50% destruction of the vertebral body and superjacent intervertebral disc, at loading intensity of 100 N. With increasing degree of destruction, the sample loses its ability to withstand the increasing loads, as evidence by a decrease of the overall deformation modulus of the samples.
Введение
Взрывные переломы тел нижнегрудного и поясничного отделов позвоночника являются наиболее распространенными среди всех повреждений позвоночника и составляют, по данным разных авторов, от 20 до 40 % всех его повреждений. Все взрывные переломы отличаются своей полиморфностью и многообразием клинических форм. Так, взрывные переломы представлены во всех делениях классификации Magerl et al. [7, 8], а именно такие, как неполный и полный взрывной перелом, взрывной перелом с дистракционным и ротационным повреждением. Также взрывные переломы являются основой хирургической классификации распределения внутренних напряжений McCormack [9], где все повреждения распределяются по таким признакам, как фрагментация тела позвонка, степень посттравматического стеноза и возможность коррекции кифотической деформации. Соответственно, полиморфность повреждений определяет возможность развития различных видов деформаций грудного и поясничного отделов позвоночника. В свою очередь, силы, воздействующие на поврежденный позвоночник, многообразны и смоделировать их все невозможно, так же как и развивающиеся под воздействием данных сил разноплоскостные деформации. Основной из них является деформация в сагиттальной плоскости — кифотическая, или угловая. Перемещения поврежденного позвоночника во всех других плоскостях возникают вслед за развитием кифотической деформации. Главной из основных смещающих сил является сила гравитационного притяжения, описанная законом всемирного тяготения [5] и действующая вдоль оси всего позвоночника.
Цель исследования: изучить биомеханические характеристики кифотической деформации, развивающейся под воздействием осевой сжимающей нагрузки, действующей вдоль всего позвоночника, в зависимости от степени повреждения позвоночных сегментов.
Материалы и методы
Предметом данного исследования является физическая модель взрывного перелома тела Th12 позвонка по классификации повреждений грудного и поясничного отделов позвоночника Magerl et al. [7, 8], соответствующая группам: А, АВ, АС. К взрывным повреждениям типа А относятся неполные взрывные переломы, неполные взрывные переломы с раскалыванием и полные взрывные переломы. Повреждения типа АВ — это дистракционные повреждения заднего костно-связочного аппарата в комбинации с взрывным переломом типа А (В 1.2.). Повреждения типа АС — ротационные повреждения — представлены полным взрывным переломом с ротацией (АС) [7, 8]. Физическая модель была выполнена на анатомических препаратах блоков позвоночных сегментов животного (свинья). Известен тот факт, что позвонки свиньи как анатомически, так и морфологически максимально приближены к позвонкам человека. Так, в работе [6] авторами проводились исследования по изучению анатомических параметров позвонков человека и свиньи (размеры тел позвонков, дуг, поперечных отростков, размеры позвоночного канала, величина физиологических искривлений). Доказано, что выполнение исследований на свиных позвонках является репрезентативным.
Эксперимент выполнялся на двух анатомических препаратах с поэтапным (4 этапа — 4 группы) разрушением структур позвоночника, вначале на одном анатомическом препарате, затем на другом, с целью получения более достоверных, усредненных результатов исследования. Первая группа была представлена позвоночными сегментами с сохраненными костными и связочными структурами (I гр. — норма). Во второй группе в модели было разрушено до 50 % тела позвонка, включая его задние отделы и один смежный межпозвоночный диск (II гр. — 50 % тела). В третьей группе в модели было разрушено все тело (100 %) и два смежных диска (III гр. — 100 % тела). В четвертой группе было разрушено тело (100 %), диски, дуги, связки и суставы (IV гр. — 100 % тела + диски + суставы + связки).
Разрушение тел позвонков и межпозвоночного диска выполняли при помощи долота. Моделируя взрывной перелом тела позвонка, мы пытались максимально приблизить экспериментальную модель к естественным условиям, а именно добиться хаотичного разрушения тела позвонка с наличием фрагментов различных размеров и с фрагментацией краниодорсальной части тела позвонка. Так, к примеру, в группе с разрушением 50 % тела позвонка (II гр.) производили несимметричное разрушение верхней части тела позвонка двумя продольными и одним поперечным рассечением. Моделируя разрушения задних отделов тела позвонка, используя продольные и поперечные рассечения, мы попытались смоделировать взрывной перелом с наличием крупного фрагмента задних отделов тела позвонка (рис. 1).
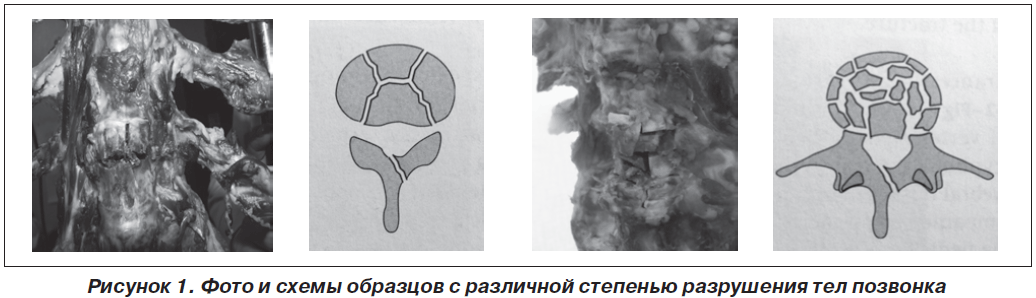
Экспериментальные исследования проводили на базе лаборатории биомеханики ГУ «ИППС им. проф. М.И. Ситенко НАМН Украины». Испытания проводили на стенде для биомеханических исследований (рис. 2). Величина деформации измерялась с помощью микрометра часового типа. Величину нагрузки измеряли с помощью тензометрического датчика SBA-100L,
результаты фиксировали устройством регистрации CAS типа CI-2001A (рис. 2).
На анатомических препаратах моделировали вертикальную осевую нагрузку. Нагрузку изменяли ступенчато, в пределах от 0 до 500 Н, с шагом 50 Н. При каждом уровне нагрузки регистрировали величину осевого сжатия. Ротационные или поперечные перемещения мы не регистрировали.
После нагрузочных тестов оценивали величину осевого сжатия и модуль общей деформации. Данные были обработаны статистически. В результате статистического анализа находили среднее значение величины сжатия модели для каждого значения нагрузки и его стандартное отклонение, после проводили расчет модуля общей деформации образцов с различной степенью разрушения позвоночного двигательного сегмента [3, 4].
Результаты и обсуждение
Рассматриваемая нами физическая модель, как любая другая модель, испытывающая нагрузки, характеризуется прочностью, жесткостью и устойчивостью ее элементов [1–3]. Исследуемый препарат как биомеханическая конструкция состоит из хрупких (кортикальная и спонгиозная кость), вязкоупругих (хрящи и межпозвоночные диски) твердых тел и упругих гибких нитей (связки). Поэтому характер его деформации при сжатии достаточно сложный [3].
При исследовании прочностных свойств системы позвоночных сегментов определялись прежде всего величина осевого сжатия и модуль общей деформации. Модуль общей деформации, как и модуль упругости, зависит от величины осевого сжатия, и его значения обратно пропорциональны величинам осевого сжатия [2] (рис. 3).
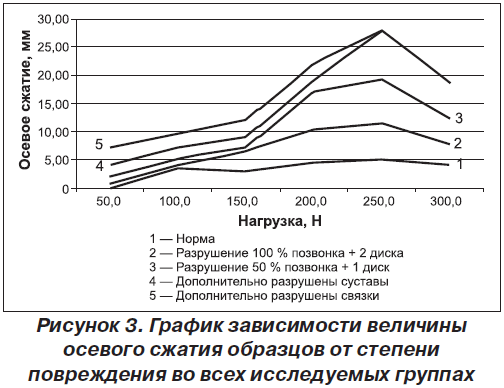
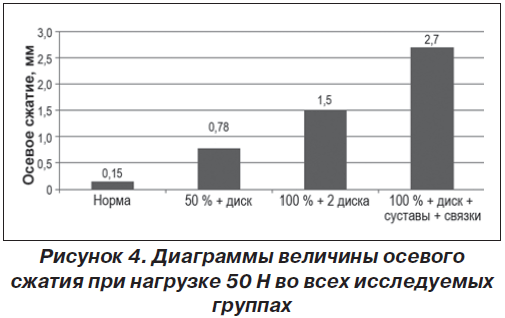
В группе I (неизмененные позвоночные сегменты) при минимальной нагрузке в 50 Н сжатие образца не превышало 0,15 мм. Образцы группы II с разрушением 50 % тела позвонка и 1 диска при данной нагрузке имели сжатие до 0,78 мм, при дальнейшем разрушении позвонков до 100 % и 2 дисков сжатие увеличивается до 1,5 мм (III группа). Достаточно заметное увеличение изменения сжатия наблюдается у образцов группы IV с дополнительно разрушенными суставами — до 2,3 мм и связками — до 3,1 мм. Результаты проведенного нами дисперсионного анализа показали, что величина осевого сжатия образцов с разной степенью повреждения статистически значимо различается. При интенсивности нагрузки в 50 Н определяется прямо пропорциональное увеличение величины осевого сжатия в зависимости от степени разрушения (рис. 4).
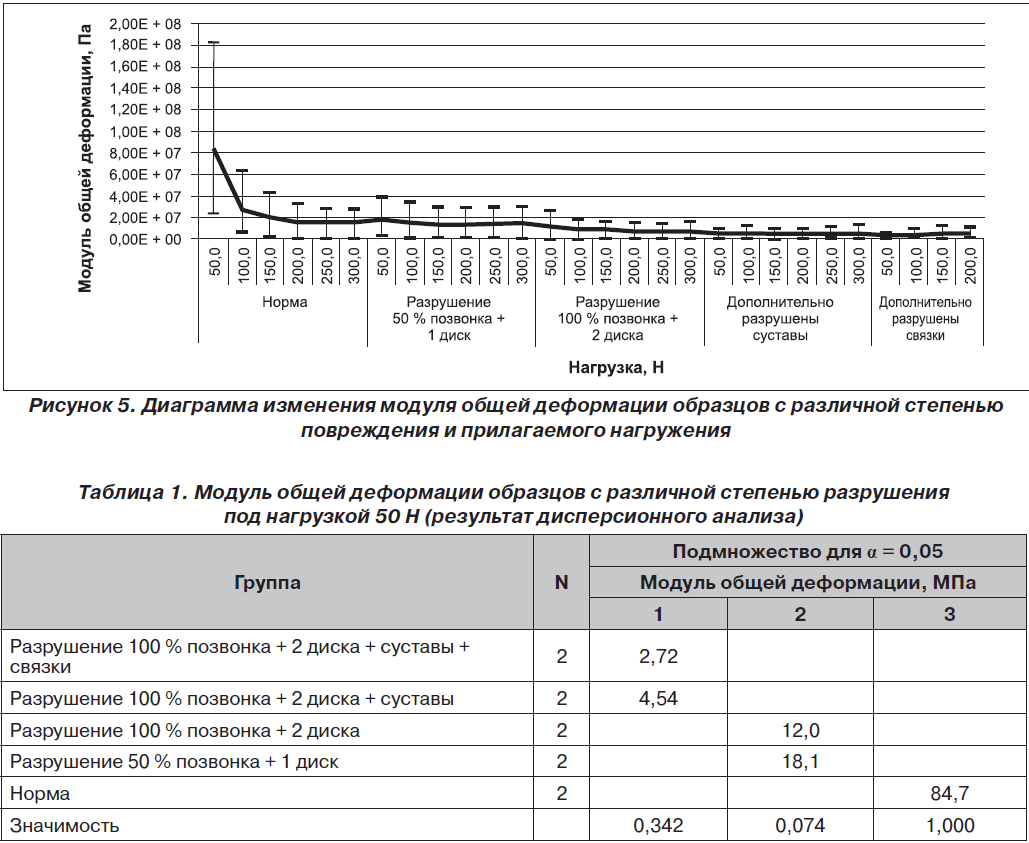
На следующем этапе работы мы проводили расчет модуля общей деформации образцов с различной степенью разрушения позвоночно-двигательного сегмента Th12 при различных нагрузках (рис. 5).
Как отмечалось ранее, по степени деформации исследуемые нами конструкции были разделены на упругие — исчезающие после устранения нагрузки и остаточные — не исчезающие [3]. Нарушение прочности наступает при возникновении остаточных деформаций. Остаточные деформации могут быть как пластического, так и хрупкого разрушения. Для костной ткани характерны остаточные деформации хрупкого разрушения, а для сумочно-связочного аппарата — остаточные деформации пластического разрушения. Таким образом, в нашем случае речь идет об остаточных деформациях хрупко-пластического разрушения. Однако в данной работе вопросы остаточных деформаций рассматриваться не будут, они станут объектом дальнейших исследований.
Так, максимальная величина модуля упругости 84,7 ± 14,8 МПа при минимальной нагрузке 50 Н была получена у целых образцов, при этом модуль упругости целого образца статистически значимо отличается от модуля общей деформации образцов (меньше в 4,5 раза) с разрушением тел позвонков 18,10 ± 2,52 МПа — разрушение 50 % и 12,00 ± 0,97 МПа — со 100% разрушением позвонка (меньше в 7 раз). Общий модуль деформации этих образцов статистически значимо отличался от образцов с дополнительно разрушенными суставами 4,5 ± 0,2 МПа и связками 2,7 ± 0,2 МПа (меньше в 18 раз и более).
Результаты дисперсионного анализа статистических различий общего модуля деформации моделей под действием нагрузки величиной 50 Н приведены в табл. 1.
Таким образом, при минимальной нагрузке во всех группах величина деформации и модуль общей деформации были прямо пропорциональны степени разрушения позвонков. В зависимости от тяжести разрушения модуль общей деформации (возможность позвоночных сегментов противостоять внешним воздействиям) в разы прогрессивно уменьшался.
При увеличении интенсивности нагрузки до 100 Н максимальные значения осевого сжатия имели образцы без повреждений. Это объясняется тем, что сохраненные структуры позвоночника остаются достаточно эластичными и величина осевого укорочения изменялась от 3,52 до 3,76 мм. Разрушение позвонков и других структур приводило к тому, что величина осевого сжатия увеличивалась, прежде всего за счет развития деформации в сагиттальной плоскости. Дальнейшее увеличение нагрузки, а именно до 100 Н в образцах II группы (разрушение тела позвонка до 50 % и вышележащего межпозвоночного диска), приводит к тому, что величина осевого сжатия увеличивается, но на минимальные значения — 0,48 мм. Дальнейшее использование нагрузки в 100 Н в группе III привело к увеличению величины осевого сжатия до 1,2 мм, а в группе IV — до 2,5 мм. Так, в группе с разрушением 50 % тела позвонка и одного диска величина осевого сжатия составила 0,48 ± 0,08 мм (рис. 6).
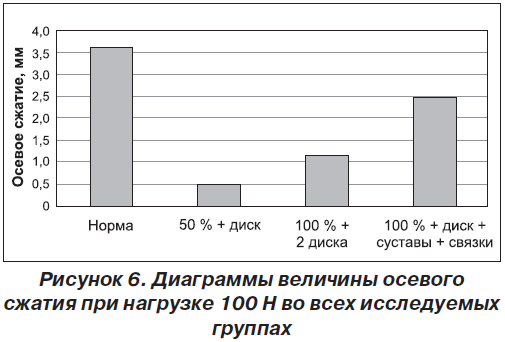
Таким образом, величина осевого сжатия составила для образцов со 100% разрушенным позвонком, 2 дисками и суставами в среднем 1,88 ± ± 0,10 мм и для образцов с дополнительно разрушенными связками — 2,98 ± 0,18 мм. При этом величина деформации образцов с частично разрушенным позвонком и диском и полностью разрушенным позвонком и 2 дисками, но сохраненным суставом и связками продолжает изменяться линейно под влиянием нагружения до 5,83 ± 0,22 мм и 6,79 ± 0,44 мм соответственно. То есть при данном объеме разрушения мы наблюдаем упругую деформацию.
Результаты дисперсионного анализа статистических отличий модуля общей деформации моделей под действием нагрузки величиной 100 Н приведены в табл. 2.
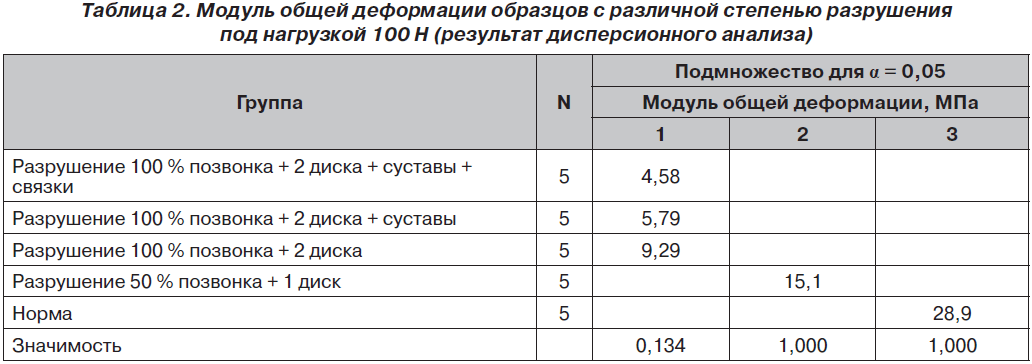
Анализируя значения модуля общей деформации при интенсивности нагружения в 100 Н, мы получили определенные закономерности. Так, при действии нагрузки 100 Н образцы с целой структурой характеризуются низким уровнем модуля общей деформации — 28,9 ± 0,5 МПа. Статистически значимо большей величиной модуля общей деформации — 15,1 ± 2,5 МПа обладают образцы с повреждением 50 % тела позвонка и вышележащего межпозвоночного диска, что противоречит принципу пропорционального уменьшения модуля общей деформации в зависимости от тяжести разрушения позвоночного сегмента. Модуль общей деформации остальных образцов в совокупности статистически значимо отличается от первых двух типов образцов, причем данный показатель прямо пропорционально уменьшается с увеличением степени повреждения образцов (III группа — 9,29 МПа; IV группа — 5,79 МПа). Феномен резкого изменения значения величины осевого сжатия в группе II с 3,76 до 0,48 мм и, соответственно, изменение модуля общей деформации с 28,9 до 15,1 МПа объясняется тем, что при интенсивности нагружения в 100 Н и при разрушении 50 % тела позвонка и вышележащего межпозвоночного диска произошло проседание поврежденных структур позвоночника, иными словами, произошло укорочение модели. Таким образом, развилась остаточная деформация, которая не устранилась после снятия нагрузки. Дальнейшее увеличение значений модуля общей деформации представлено его упругой составляющей. Можно сделать вывод, что на этапе разрушения 50 % тела позвонка и вышележащего межпозвоночного диска при интенсивности нагружения 100 Н произошло нарушение прочности модели.
Рассчитать общий модуль деформации для больших нагрузок не представляется возможным из-за выпадения из эксперимента некоторых образцов с полным разрушением тела позвонка, двух дисков, дуг и связок по причине возникшей пластической деформации.
Дальнейшее увеличение нагрузки до 150 Н было достаточным, чтобы максимально сжать образцы с полностью разрушенными структурами, и дальнейшее увеличение нагрузки до 200 Н практически не изменило их осевые размеры.
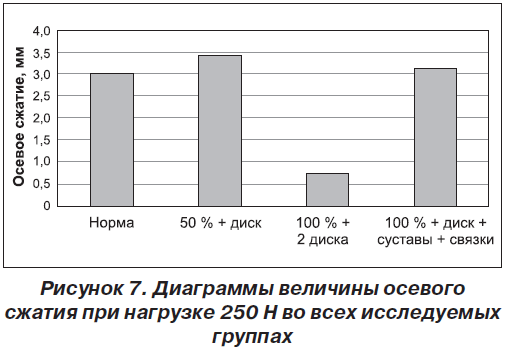
Увеличение нагрузки до 250 Н приводит к возникновению пластических деформаций в образцах с полностью разрушенными задними структурами. Образцы с неразрушенной задней структурой могут выдерживать нагрузку в 250 Н с осевым сжатием на уровне 4,93 ± 1,21 мм, все остальные образцы изменяют линейные размеры примерно одинаково, в пределах от 6,56 до 8,64 мм, причем чем больше разрушений, тем больше линейное изменение длины образца.
Уменьшение величин осевого сжатия поврежденных образцов под нагрузкой больше 250 Н объясняется тем, что образец достиг предела сжатия под меньшей нагрузкой и дальнейшее уменьшение сжатия осуществляется за счет других механизмов — ротации, изгиба и т.д., однако эти искривления очень незначительны и не являются значимыми (рис. 7).
Таким образом, можно сделать заключение, что при увеличении объема разрушений позвоночно-двигательного сегмента Th12 величина укорочения модели под действием сжимающих нагрузок статистически достоверно увеличивается при всех величинах сжимающей силы. В зависимости от степени разрушения и величины прилагаемой нагрузки встречаются как упругие, так и пластические деформации.
Выводы
1. При увеличении объема разрушений позвоночно-двигательного сегмента Th12 величина осевого сжатия модели под действием сжимающих нагрузок статистически достоверно увеличивается при всех величинах сжимающей силы.
2. В зависимости от степени разрушения позвоночно-двигательного сегмента Th12 модуль общей деформации модели снижается за счет выпадения из опорной функции элементов сегмента.
3. В зависимости от степени разрушения и величины прилагаемой нагрузки встречаются как упругие, так и пластические виды деформации. Нарушение прочности модели произошло на этапе разрушения 50 % тела позвонка и вышележащего межпозвоночного диска при интенсивности нагружения 100 Н. С увеличением степени разрушения образец теряет способность противостоять возрастающим нагрузкам, что подтверждается уменьшением модуля общей деформации исследуемых образцов.
Конфликт интересов. Авторы заявляют об отсутствии какого-либо конфликта интересов при подготовке данной статьи.